Distribuição de Probabilidade Binomial
Hoje vamos estudar uma variável aleatória específica que gera uma distribuição de probabilidade muito utilizada em problemas do dia a dia de qualquer profissional: a distribuição Binomial.
Conceito
Uma distribuição de probabilidade binomial resulta de um experimento que satisfaz os seguintes requisitos:
1. O experimento tem um número finito de tentativas.
2. As tentativas devem ser independentes (o resultado de qualquer tentativa individual não afeta as probabilidades nas outras tentativas).
3. Cada tentativa deve ter todos os resultados classificados em duas categorias (em geral, chamadas de sucesso e fracasso).
4. A probabilidade de sucesso permanece constante em todas as tentativas.
Indo para a prática
Para exemplificar, vamos falar do número de vezes que sai o número 5 no lançamento de dois dados. Observe que nesse caso temos satisfeitos os quatro requisitos da definição de probabilidade binomial:
O lançamento de dois dados pode ser interpretado como dois (número finito) lançamentos.
O resultado do primeiro lançamento do dado não interfere no resultado do segundo lançamento, por isso são classificados como independentes.
Cada lançamento pode resultar em um sucesso (sair 5) ou em um fracasso (sair um número diferente de 5).
A probabilidade de sair 5 é sempre igual a 1/6 em cada um dos lançamentos.
Em qualquer distribuição binomial, a probabilidade de ocorrência de sucessos em um conjunto de tentativas pode ser calculada a partir da expressão seguinte:
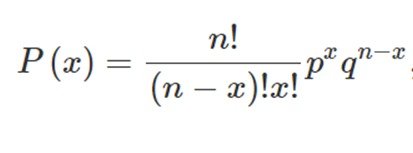
Figura 1. Formula do calculo de probabilidade na distribuição binomial
sendo:
p= a probabilidade de sucesso em uma tentativa;
q= a probabilidade de fracasso em uma tentativa;
n= o número de tentativas;
x= a quantidade de sucesso nas n tentativas.
Exemplo
No lançamento de dois dados não viciados, qual é a probabilidade de ocorrência de exatamente UM resultado igual a 5?
Solução:
Nesse exemplo, temos que n=2 (dois lançamentos), x=1 (um sucesso), p=1/6 e q= 1 – 1/6 = 5/6.
Aplicando a equação A, temos:

Figura 2. Resultado da questão
Média, Variância e Desvio Padrão
Agora já sabemos identificar distribuições binomiais e calcular suas probabilidades,então agora vamos aprender a determinar as principais medidas de tendência central e dispersão.
A tabela abaixo apresenta as fórmulas para os cálculos de média, variância e desvio-padrão nas distribuições binomiais.

Figura 3. Medidas de tendência central e dispersão para uma distribuição binomial
Para exercitar, vamos calcular a média, a variância e o desvio-padrão para a variável aleatória X que corresponde ao número de vezes que sai o número 5 no lançamento de dois dados.
Média
mu = np = 2⋅1/6 ≃ 0,33 vezes
Variância
σ2 = npq = 2⋅1/6⋅5/6 ≃ 0,28 vezes ao quadrado
Desvio padrão
σ = √0,28 ≃ 0,53 vezes
No meu Curso de Estatística eu ensino como aplicar estatística com autonomia e ser um profissional mais qualificado. Caso queira saber os detalhes do conteúdo do curso, basta clicar aqui.
Espero ter ajudado! Leia também nosso texto sobre p-valor.
Referências
UNIVESP. Estatística – Aula 11 – Distribuições de Probabilidade. 2015. Disponível em: https://www.youtube.com/watch?v=j3Zbup0KMxY . Acesso em: 22 mar. 2022.
TRIOLA, M. F. Introdução à Estatística: atualização da tecnologia, v. único. 11. ed. Rio de Janeiro: LTC, 2013.
Pesquise o assunto desejado em estatística no campo abaixo
© 2021 Prof. Fernanda Maciel
contato@proffernandamaciel.com
